Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
Determine the equations of the following parabolas and indicate the values of their focal parameter, focus and directrix.
1 
2 
Exercise 2
Determine the equations of the parabolas using the information given:
1 The directrix is x = −3 and the focus is (3, 0).
2 The directrix is y = 4 and the vertex is (0, 0).
3 The directrix is y = −5 and the focus is (0, 5).
4 The directrix is x = 2 and the focus is (−2, 0).
5 The focus is (2, 0) and the vertex is (0, 0).
6 The focus is (3, 2) and the vertex is (5, 2).
7 The focus is (−2, 5) and the vertex is (−2, 2).
8 The focus is (3, 4) and the vertex is (1, 4).
Exercise 3
Calculate the vertex, focus and directrix of the following parabolas:
1 
2 
3 
Exercise 4
Find the equation of the vertical parabola that passes through the points: A = (6, 1), B = (−2, 3) and C = (16, 6).
Exercise 5
Determine the equation of the parabola with a directrix of y = 0 and a focus at (2, 4).
Exercise 6
Determine the point(s) of intersection between the line r ≡ x + y − 5 = 0 and the parabola y² = 16x.
Exercise 7
Find the equation of the horizontal parabola that passes through the point (3, 4) and has its vertex at (0, 0).
Exercise 8
Determine the equation of the parabola with an axis parallel to the y-axis, vertex on the x-axis and which passes through the points A = (2, 3) and B = (−1, 12).
Exercise 9
Determine the equation of the parabola with a directrix of x + y − 6 = 0 and a focus at (0, 0).
Solution of exercise 1
Determine the equations of the following parabolas and indicate the values of their focal parameter, focus and directrix.
1 







2 



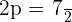



3 







Solution of exercise 2
Determine the equations of the parabolas using the information given:
1 The directrix is x = −3 and the focus is (3, 0).



2 The directrix is y = 4 and the vertex is (0, 0).



3 The directrix is y = −5 and the focus is (0, 5).



4 The directrix is x = 2 and the focus is (−2, 0).



5 The focus is (2, 0) and the vertex is (0, 0).



6 The focus is (3, 2) and the vertex is (5, 2).



7 The focus is (−2, 5) and the vertex is (−2, 2).



8 The focus is (3, 4) and the vertex is (1, 4).


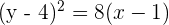
Solution of exercise 3
Calculate the vertex, focus and directrix of the following parabolas:
1 











2 











3 

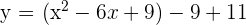









Solution of exercise 4
Find the equation of the vertical parabola that passes through the points: A = (6, 1), B = (−2, 3) and C = (16, 6).








Solution of exercise 5
Determine the equation of the parabola with a directrix of y = 0 and a focus at (2, 4).




Find various Maths tutor on Superprof.
Solution of exercise 6
Determine the point(s) of intersection between the line r ≡ x + y − 5 = 0 and the parabola y² = 16x.








Solution of exercise 7
Find the equation of the horizontal parabola that passes through the point (3, 4) and has its vertex at (0, 0).




Solution of exercise 8
Determine the equation of the parabola with an axis parallel to the y-axis, vertex on the x-axis and which passes through the points A = (2, 3) and B = (−1, 12).
Axis parallel to the y-axis 
Vertex on the x-axis 








Solution of exercise 9
Determine the equation of the parabola with a directrix of x + y − 6 = 0 and a focus at (0, 0).
















There are errors with the answers. The 2y was squared during the substitutions, similar things occuring throughout the examples
In my opinion there are mistakes while substituting “y” into circle formula.
It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
This is very nice but please show how to find the 4p
It’s already been in the formula, but if you reffering why the 4p was used in the formula try take chat with deepseek, it was a good gpt alternatives even better for math
Hi Enabel! Thanks for sharing this helpful advice!