Encuentra la ecuación de la recta con pendiente 5 y que pasa por el punto 
Empleamos la fórmula punto - pendiente de una recta:
Si sustituimos los datos conocidos, la ecuación de la recta es:
Por lo tanto, la ecuación de la recta es:
Encuentra la ecuación de la recta con pendiente -3 y que pasa por el punto 
Empleamos la fórmula pendiente-ordenada al origen de una recta:
Si sustituimos los datos conocidos, la ecuación de la recta es:
Por lo tanto, la ecuación de la recta es:
Encuentra la ecuación de la recta que pasa por los punto y 
Buscamos la pendiente de la recta:
Empleamos la fórmula pendiente-ordenada al origen de una recta:
Si sustituimos los datos conocidos, la ecuación de la recta es:
Por lo tanto, la ecuación de la recta es:
Hallar la ecuación de la recta que pasa por 
y es paralela a la recta 
Encontramos la pendiente de la recta
Como la recta que pasa por es paralela a la recta, entonces ambas tienen la misma pendiente 
Sustituimos la pendiente y el punto por donde pasa la recta en la ecuación punto-pendiente y obtenemos
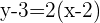
Por lo tanto, la ecuación de la recta es:
Hallar la ecuación de la recta que pasa por 
y es perpendicular a la recta 
Encontramos la pendiente de la recta
Como la recta que pasa por es perpendicular a la recta, entonces su pendiente es 
Sustituimos la pendiente y el punto por donde pasa la recta en la ecuación punto-pendiente y obtenemos
Por lo tanto, la ecuación de la recta es:
Determina si las rectas 
y 
son paralelas, perpendiculares o ninguna de las dos.
Encontramos la pendiente de la recta
Encontramos la pendiente de la recta
Como 
, entonces las rectas no son paralelas.
Como 
, entonces las rectas no son perpendiculares.
Por tanto, las rectas no son paralelas ni perpendiculares.
Determina si las rectas 
y 
son paralelas, perpendiculares o ninguna de las dos.
Encontramos la pendiente de la recta
Encontramos la pendiente de la recta
Como , entonces las rectas no son paralelas.
Como 
, entonces las rectas son perpendiculares.
Determina si las rectas 
y 
son paralelas, perpendiculares o ninguna de las dos.
Encontramos la pendiente de la recta
Encontramos la pendiente de la recta 
Como 
, entonces las rectas son paralelas.
Escribe de todas las formas posibles la ecuación de la recta que pasa por los puntos 
y 
.
Tenemos que la recta para por los puntos y . Por lo tanto, el vector que une estos dos puntos es:
Con estos datos ya podemos obtener las ecuaciones de la recta (las fórmulas se pueden consultar en nuestro artículo "Resumen de ecuaciones de la recta").
Ecuación de la recta que pasa por 2 puntos:
Ecuación vectorial:
Ecuaciones paramétricas:
Ecuación continua:
Ecuación general:
Ecuación explícita:
Ecuación punto-pendiente:
De un paralelogramo 
conocemos 
. Halla las coordenadas del vértice D.
Antes de encontrar las coordenadas del vértices observemos la siguiente figura:
Sabemos que el vector que va de 
a 
debe ser igual al vector que va de 
a 
, es decir:
Realizamos los cálculos:
donde 
es la coordenada x del punto , y 
es su coordenada y. De este modo, tenemos:
Por lo tanto, el punto es
Clasificar el triángulo determinado por los puntos: 
y 
Para clasicar el triángulo primero debemos calcular la distancia de cada uno de sus lados. Eso lo hacemos de la siguiente manera:
Notemos que se cumple que:
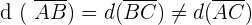
Por lo tanto, el triángulo es isósceles. Además, se cumple también que
De manera que el triángulo también es rectángulo. Esto se puede apreciar en la siguiente figura:
Hallar la pendiente y la ordenada en el origen de la recta 
Tenemos la ecuación . Despejamos 
de la ecuación:
A partir de aquí podemos ver que la pendiente es:
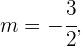
Mientras que la ordenada al origen es:
Estudiar la posición relativa de las rectas de ecuaciones:
a 
b 
c 
d 
Notemos que los coeficientes de la recta 1 y 2 son proporcionales:
Por lo tanto, la recta 1 y 2 son coincidentes (son la misma recta).
Asimismo, notemos que los coeficientes de 
e de la recta 1 y 3 son proporcionales, sin embargo, los términos independientes no son proporcionales:
Por lo tanto, la rectas 1 y 3 son paralelas. En consecuencia, las rectas 2 y 3 son paralelas (ya que 1 y 2 son iguales).
Finalmente, observemos que los coeficientes para e de la recta 4 no son proporcionales a los coeficientes de ninguna otra recta:
Por lo tanto, la recta 4 es secante a las rectas 1, 2 y 3.
Hallar la ecuación de la recta 
, que pasa 
, y es paralela a la recta 
Observemos la siguiente figura de dos rectas paralelas:
Sabemos que dos rectas son paralelas si sus pendientes son la misma:
Por lo tanto, la recta tiene la forma (punto-pendiente):
Igualando a 0, tenemos que la recta se puede escribir como:
Se tiene el cuadrilátero cuyos vértices son 
y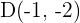 
. Comprueba que es un paralelogramo y determina su centro
Para que el cuadrilátero sea un paralelogramo debemos tener que: 
y
Notemos que:
Por lo tanto, se cumple que . Por otro lado, tenemos que:
Así, el cuadrilátero es un paralelogramo.
Ahora debemos encontrar el punto medio. Sabemos que las diagonales se cortan en el punto medio (y este punto es el centro del paralelogramo), por lo tanto basta encontrar el punto medio de alguna de las diagonales. El punto medio de la diagonal \bar{AC} es
Así, el centro es el punto 
. Observemos la figura del paralelogramo:
Hallar la ecuación de la recta que pasa por el punto 
y es paralela a la recta que une los puntos 
y 
Si 
es la recta que une los puntos, entonces sabemos que la recta que buscamos es paralela a . Por lo tanto, tienen la misma pendiente:
Si utilizamos la forma punto-pendiente de la recta, entonces la ecuación de la recta es:
Por lo tanto, la ecuación de la obtenemos igualando a cero:
Los puntos 
y 
, son vértices de un triángulo isósceles 
que tiene su vértice en la recta 
siendo 
y 
los lados iguales. Calcular las coordenadas del vértice
Escribamos las coordenadas del punto como 
. Como 
, entonces tenemos que se cumple:
Si despejamos 
, tenemos que
Además, los lados y son iguales, por lo que se cumple 
.
Si elevamos al cuadrado, tenemos:
Si sustituimos el valor entonces tenemos:
Si expandimos el polinomio y resolvemos la ecuación "cuadrática" (al final los términos cuadráticos se cancelan), tenemos,
Por último, sustituyendo este valor de 
en la ecuación para nos da:
Por lo tanto, el punto es 
. La gráfica del triángulo es la siguiente:
La recta 
pasa por el punto 
y es paralela a la recta 
. Calcula 
y 
Sabemos que 
para por . Por lo tanto, al sustituir las coordenadas del punto se sigue satisfaciendo la igualdad:
Además, sabemos que 
, por lo que los coeficientes son proporcionales:
Por lo tanto, 
Dado el triángulo , de coordenadas 
y 
; calcula la ecuación de la mediana que pasa por el vértice
Tenemos el siguiente triángulo y deseamos calcular la mediana graficada:
Sabemos que la mediana pasará por el punto medio del segmento 
. Por tanto, calculamos las coordenadas de este punto (que denotaremos como 
):
Ahora escribimos la ecuación de la que pasa por y (usamos la fórmula de la recta que pasa por dos puntos):
Simplificando un poco, obtenemos la siguiente ecuación:
De un paralelogramo se conoce un vértice, 
, y el punto de corte de las dos diagonales, 
. También sabemos que otro vértice se encuentra en el origen de coordenadas. Calcular:
a Los otros vértices.
b Las ecuaciones de las diagonales.
c La longitud de las diagonales.
Vamos resolviendo cada uno de los incisos:
a Los otros vértices:
Sabemos que 
es el punto medio de 
, por tanto, tenemos:
De aquí se sigue que:
Por lo tanto, 
. Asimismo, es el punto medio de 
, por lo que tenemos:
De aquí se sigue que:
De este modo, 
. Así, los cuatro vértices son los puntos 
y 
.
b Las ecuaciones de las diagonales.
En este caso sólo tenemos que utilizar la fórmula de la recta que pasa por dos puntos. Primero para la diagonal :
Simplificando un poco obtenemos 
. Luego, para la diagonal 
tenemos:
Que, después de simplificar, obtenemos 
.
cLa longitud de las diagonales.
Para calcular la longitud de las diagonales basta con calcular la distancia entre los vértices apropiados. Para la diagonal tenemos:
Mientras que para la diagonal la longitud es:
La gráfica del paralelogramo es la siguiente:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar las ecuaciones parametricas del plano x-2y+z-1=0
Hola, me sirvio mucho, con que informacion podria ponerlos como refernecia en mi proyecto?
Hola que bueno que la pagina te ayudo, podrías poner como pagina de internet «Materíal didactico-Superprof».
– Hallar la ecuación de la recta en su forma simétrica que tiene pendiente igual a 3/2 y que intersecta al eje «y» en (0.2)
Buenas tardes,
Me han ayudado muchísimo vuestros apuntes. Sólo tengo una consulta, ¿cómo tendría que calcular la pendiente de una recta en 3 dimensiones, es decir, en el espacio cartesiano (x, y, z)?
En tres dimensiones no se usa la pendiente pues como se usan tres ejes todo cambia, sino más bien el ángulo que se calcula con el vector director de la recta.
Calcule el angulo que forman las rectas A y B sabiendo que sus vectores directores son A(-3,5) B(2,-5)