Capítulos
- Regla de L'Hôpital
- Ejercicios resueltos de la regla de L'Hôpital
- Formas de Indeterminaciones en potencias
- Ejercicios resueltos con indeterminaciones
- Ejercicios resueltos de la indeterminacion infinito menos infinito
- Indeterminación cero por infinito
- Ejercicios diversos de indeterminaciones y regla de L'Hôpital
La regla de L'Hôpital es un importante teorema en cálculo diferencial que se utiliza para evaluar límites indeterminados de funciones. Fue desarrollada por el matemático francés Guillaume de L'Hôpital en el siglo XVIII. Esta regla proporciona un método efectivo para calcular límites de la forma 
o 
, que son formas indeterminadas.
La regla de L'Hôpital es una herramienta muy útil para simplificar cálculos y resolver límites que de otro modo serían difíciles de calcular. Sin embargo, es importante recordar que solo se aplica en situaciones específicas donde se cumplen las condiciones necesarias.
Regla de L'Hôpital
Si 
y 
son 2 funciones continuas tal que
La regla de L'Hôpital nos dice que
.
Para poder aplicar la regla de L'Hôpital hay que tener un límite de la forma 
, y tener una de las siguientes indeterminaciones
,
A continuación unos ejercicios resueltos para poder entender de manera más clara
Ejercicios resueltos de la regla de L'Hôpital
1 Identificar indeterminación
2 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
3 Obtener el límite
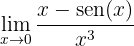
1 Identificar indeterminación
2 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
Obtenemos nuevamente una indeterminación por lo que aplicaremos la regla de L'Hôpital otra vez
Una vez más
3 Obtener el límite
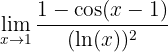
1 Identificar indeterminación
2 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
Volvemos a aplicar la regla
3 Obtener el límite
1 Identificar indeterminación
2 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
Utilizamos la siguiente propiedad de la funciones trigonométricas 
, y volvemos aplicar la regla de L'Hôpital
3 Obtener el límite
1 Identificar indeterminación
2 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
3 Obtener el límite
Formas de Indeterminaciones en potencias
Las formas indeterminadas 
, 
y 
se obtienen cuando consideramos expresiones de la forma
Estas indeterminaciones se resuelven primero aplicando propiedades del logaritmo:
Tengo mi función
Aplico logaritmo
Aplico exponencial
Entonces
Por lo que para resolver el límite inicial, me basta con obtener el límite de su logaritmo
Y así, el límite original será
Ejercicios resueltos con indeterminaciones
1 Identificar indeterminación
2 Tomamos límite del logaritmo
Tenemos forma indeterminada
3 Aplicar regla de L'Hôpital
Forma indeterminada
Aplicamos regla de L'Hôpital de nuevo
4 Obtenemos el límite
Por lo tanto
Y entonces
1 Identificar indeterminación
2 Tomamos límite del logaritmo
Tenemos forma indeterminada
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
Entonces
4 Obtenemos el límite original
Por lo tanto
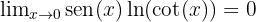
Y entonces
1 Identificar indeterminación
2 Tomamos límite del logaritmo
Tenemos forma indeterminada
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
Entonces
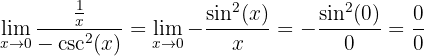
Aplicamos L'Hôpital de nuevo
4 Obtenemos el límite original
Por lo tanto
Y entonces
1 Identificar indeterminación
2 Tomamos límite del logaritmo
Tenemos forma indeterminada
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
Entonces
4 Obtenemos el límite original
Por lo tanto
Y entonces
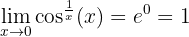
1 Identificar indeterminación
2 Calculamos el límite del logaritmo
Tenemos forma indeterminada
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
4 Obtenemos el límite original
Por lo tanto
Y entonces
Ejercicios resueltos de la indeterminacion infinito menos infinito
En estos casos tenemos que tener en ver que tan "rápido" las funciones se van a infinito. Además si son fracciones, se ponen a común denominador.
1 Identificar indeterminación
2 Reescribimos la expresión
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
Obtengo otra indeterminación, por lo que vuelvo a aplicar la regla
4 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Reescribimos la expresión
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
Obtengo otra indeterminación, por lo que vuelvo a aplicar la reglar
4 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Reescribimos la expresión
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
Obtengo otra indeterminación, por lo que vuelvo a aplicar la reglar
4 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Reescribimos la expresión
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
Obtengo otra indeterminación, por lo que vuelvo a aplicar la regla
4 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Reescribimos la expresión
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
4 Obtenemos el límite
Por lo tanto
Indeterminación cero por infinito
Estas formas de indeterminación se pueden transformar a casos que ya vimos, como ó .
Como se muestra a continuación, tenemos que
donde 
y 
Entonces lo podemos reescribir de tal manera que sea más fácil sacar la derivada
ó
Teniendo esto ya podemos usar la regla de L'Hôpital
Ejercicios resueltos de la indeterminación cero por infinito
1 Identificar indeterminación
2 Reescribimos la expresión
Indeterminación de tipo
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
4 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Reescribimos la expresión
Indeterminación de tipo
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
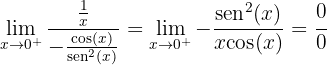
Aplicamos de nuevo la regla de L'Hôpital
4 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Reescribimos la expresión
Indeterminación de tipo
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
Aplicamos de nuevo la regla de L'Hôpital
4 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Reescribimos la expresión
Expresamos lo mismo de una manera conveniente para poder aplicar la regla de L'Hôpital
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
4 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Reescribimos la expresión
Indeterminación de tipo
3 Aplicar regla de L'Hôpital
Al derivar obtenemos
4 Obtenemos el límite
Por lo tanto
Ejercicios diversos de indeterminaciones y regla de L'Hôpital
1 Identificar indeterminación
2 Aplicar regla de L'Hôpital
Al derivar obtenemos
3 Obtenemos el límite
Por lo tanto
1 Identificar indeterminación
2 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
3 Obtener el límite
1 Identificar indeterminación
2 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
3 Obtener el límite
1 Identificar indeterminación
2 Reformulación del problema
Solo expresando de diferente manera podremos encontrar las condiciones para aplicar regla de L'Hôpital
3 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
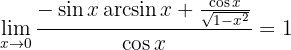
4 Obtener el límite
1 Identificar indeterminación
2 Calculamos el límite del logaritmo
Tenemos forma indeterminada
3 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
4 Obtener el límite
1 Identificar indeterminación
2 Calculamos el límite del logaritmo
Tenemos forma indeterminada
3 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
Aplicamos la regla de lopital otra vez
4 Obtener el límite
1 Identificar indeterminación
2 Aplicar la regla de L'Hôpital
Derivamos el númerador y denominador del cociente. Tomamos límite.
Aplicamos la regla de L'Hôpital otra vez
3 Obtener el límite
1 Identificar indeterminación
2 Reescribimos la expresión
Indeterminación
3 Aplicar la regla de L'Hôpital
Aplicamos la regla de L'Hôpital otra vez
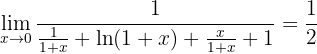
4 Obtener el límite
1 Identificar indeterminación
2 Tomamos límite del logaritmo
Tenemos forma indeterminada
3 Aplicar la regla de L'Hôpital
4 Obtener el límite original
1 Identificar indeterminación
2 Tomamos límite del logaritmo
Rescribimos de manera conveniente
Tenemos forma indeterminada
3 Aplicar la regla de L'Hôpital
Aplicamos la regla de L'Hôpital otra vez
4 Obtener el límite original
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Nose como se arrastra la imagen
Hola, nos encantaría poder ayudarte pero podrías mencionar el número del ejercicio y te diremos como puedes arrastrar la imagen al lugar que deseas.
Representar gráficamente la curva Inversión Ahorro cuando hay una política fiscal de incremento del gasto público
la uno esta mal el vertice no es (0,0) es (0,3)
Una disculpa ya se corrigió.