El análisis de asíntotas es crucial para entender el comportamiento de las funciones en los extremos de su dominio y en puntos críticos donde la función puede volverse infinita o indeterminada. A través de estos ejercicios resueltos, exploraremos cómo encontrar asíntotas horizontales, verticales y oblicuas, utilizando técnicas algebraicas y de cálculo.
Cada ejercicio será desglosado paso a paso, ilustrando las estrategias para identificar las asíntotas de diversas funciones.
Hallar las asíntotas horizontales, verticales y oblicuas en cada uno de los siguientes ejercicios:

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que tiene una asíntota horizontal  .
.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es la asíntota horizontal

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que la asíntota horizontal es  .
.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es la misma que la asíntota horizontal

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que la asíntota horizontal es  .
.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es la msima que la asíntota horizontal 

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que la asíntota horizontal es  .
.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es la misma que la asíntota horizontal 
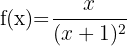
1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 
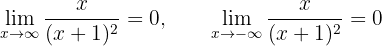
Concluimos que tiene asíntota horizontal  .
.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es la misma que la horizontal 

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que la asíntota horizontal es  .
.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es la misma que la horizontal 

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que la asíntota horizontal es  .
.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 


La función tiene asíntotas verticales 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es la misma que la horizontal 

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que no existen asíntotas horizontales.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es 

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que no existen asíntotas horizontales.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas
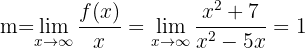

La asíntota oblícua es 

1 Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que no existen asíntotas horizontales.
2 Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
3 Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas
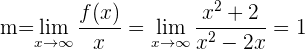

La asíntota oblícua es 

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que no existen asíntotas horizontales.
Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La asíntota oblícua es 

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que no existen asíntotas horizontales.
Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas

La función no posee asíntotas oblícuas

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que no existen asíntotas horizontales.
Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota vertical 
Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La función posee asíntota oblícua 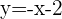

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota horizontal en 
La función no posee asíntotas verticales ni oblícuas.

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

La función tiene una asíntota horizontal en 
La función no posee asíntotas verticales ni oblícuas.

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

Concluimos que no existen asíntotas horizontales.
Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene asíntotas verticales 
Asíntota oblícua
Calculamos mediante límites le pendiente y ordenada al origen de las asíntotas oblícuas


La función posee asíntota oblícua 

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

La función tiene asíntota horizontal 
Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene asíntota vertical 
La función no posee asíntotas oblícuas

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

La función tiene asíntota horizontal 
La función no posee asíntotas verticales ni oblícuas.

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

La función tiene asíntota horizontal 
La función no posee asíntotas verticales ni oblícuas.

Asíntota horizontal
Calculamos los límites cuando  tiende a
tiende a 

La función tiene asíntota horizontal 
Asíntota vertical
Calculamos los límites cuando  tiende a
tiende a 

La función tiene asíntota vertical 
La función no posee asíntotas oblícuas



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Nose como se arrastra la imagen
Hola, nos encantaría poder ayudarte pero podrías mencionar el número del ejercicio y te diremos como puedes arrastrar la imagen al lugar que deseas.
Representar gráficamente la curva Inversión Ahorro cuando hay una política fiscal de incremento del gasto público
la uno esta mal el vertice no es (0,0) es (0,3)
Una disculpa ya se corrigió.