Capítulos
Los sistemas de ecuaciones de dos variables son una herramienta fundamental en matemáticas, utilizados en diversas áreas como la economía, la física y la ingeniería. Estos sistemas consisten en dos ecuaciones lineales que se deben resolver simultáneamente para encontrar el valor de las dos incógnitas. Resolver un sistema de ecuaciones 2x2 permite determinar puntos de intersección en un plano cartesiano, proporcionando soluciones que pueden ser únicas, infinitas o inexistentes.

Resolución por sustitución y método gráfico
Resuelve el siguiente sistema utilizando el método de sustitución

El método de sustitución involucra despejar una de las dos variables de alguna ecuación y sustituirla en la otra. Despejaremos  de la segunda ecuación:
de la segunda ecuación:

Notemos que escogimos la segunda ecuación ya que está igualada a 0; esto hace el procedimiento ligeramente más sencillo. Ahora sustituimos el valor de  en la primera ecuación
en la primera ecuación

Por lo tanto,  . Luego, sustituimos el valor de
. Luego, sustituimos el valor de  en la expresión que tenemos para
en la expresión que tenemos para  :
:

Por tanto, la solución es  .
.
Resuelve el siguiente sistema utilizando el método de sustitución:

Una ventaja del método de sustitución es que no es necesario simplificar el sistema de ecuaciones para empezar a resolver. Por tanto, podemos empezar a resolver inmediatamente.
Primero, despejamos  de la segunda ecuación:
de la segunda ecuación:
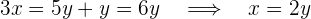
Luego, sustituimos el valor de  en la primera ecuación:
en la primera ecuación:

De aquí, se sigue que  . Ahora, sustituimos el valor de
. Ahora, sustituimos el valor de  en la expresión que teníamos para
en la expresión que teníamos para  :
:

Por tanto, la solución al sistema es  y
y  .
.
Resuelve el siguiente sistema utilizando el método de sustitución:

Primero despejamos  de la segunda ecuación
de la segunda ecuación

Luego, sustituimos el valor de  en la primera ecuación:
en la primera ecuación:

Por lo tanto, la primera ecuación se convierte (al pasar las constantes del lado derecho y las variables del lado izquierdo) en

que, al despejar  , obtenemos
, obtenemos

Luego, sustituyendo el valor de  en la expresión que tenemos para
en la expresión que tenemos para  , obtenemos
, obtenemos

Por tanto, la solución es  y
y 
Resuelve el siguiente sistema utilizando el método de sustitución:

Para resolver este sistema, primero debemos eliminar las fracciones (quitar los denominadores). Para ello, multiplicamos las ecuaciones por el mínimo común multiplo de los denominadores. Para la primera ecuación tenemos:

por lo que  . Mientras que para la segunda ecuación tenemos:
. Mientras que para la segunda ecuación tenemos:

de donde obtenemos  . Así, el sistema de ecuaciones se convierte en:
. Así, el sistema de ecuaciones se convierte en:

Primero despejamos  de la segunda ecuación:
de la segunda ecuación:

Luego, sustituimos el valor de  en la primera ecuación:
en la primera ecuación:

de modo que  o
o  . Luego, sustituimos el valor de
. Luego, sustituimos el valor de  en la expresión que teníamos para
en la expresión que teníamos para  :
:

Por tanto, la solución es  y
y  .
.
Resuelve el siguiente sistema utilizando el método gráfico

El método gráfico involucra solo graficar las dos rectas. La intersección será la solución del sistema:

De la gráfica anterior podemos observar que la solución es  y
y  . No obstante, recordemos que debemos ser muy precisos al momento de graficar.
. No obstante, recordemos que debemos ser muy precisos al momento de graficar.
Resolución por igualación
Recordemos que el método de igualación sólo se puede utilizar para resolver un sistema de 2 ecuaciones con 2 variables. Solamente este método y el método gráfico están limitados para sistemas de  .
.

Para resolver el sistema por igualación debemos despejar una variable de ambas ecuaciones. Despejamos  de ambas ecuaciones:
de ambas ecuaciones:

de donde obtenemos  . Para la segunda ecuación tenemos
. Para la segunda ecuación tenemos

por tanto  y
y  . Ahora, igualamos ambas ecuaciones
. Ahora, igualamos ambas ecuaciones

De esa ecuación despejamos  :
:

por lo que  . Luego, sustituimos el valor de
. Luego, sustituimos el valor de  en la primera ecuación
en la primera ecuación

por lo que  . Por tanto, la solución es
. Por tanto, la solución es  y
y  .
.

Al igual que en el caso anterior, para resolver por igualación debemos despejar alguna variable de ambas ecuaciones. En este caso despejaremos  . En la primera ecuación obtenemos:
. En la primera ecuación obtenemos:

Mientras que para la segunda ecuación obtenemos:

Igualando las ecuaciones, tenemos

por lo que

de manera que  . Luego, sustituyendo
. Luego, sustituyendo  en la primera ecuación, tenemos
en la primera ecuación, tenemos

por lo que  . Así, la solución es
. Así, la solución es  y
y  .
.

Al igual que en el caso anterior, para resolver por igualación debemos despejar alguna variable de ambas ecuaciones. En este caso despejaremos  . En la primera ecuación obtenemos:
. En la primera ecuación obtenemos:
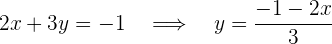
Mientras que para la segunda ecuación obtenemos:

Igualando las ecuaciones, tenemos

por lo que

de manera que  . Luego, sustituyendo
. Luego, sustituyendo  en la segunda ecuación, tenemos
en la segunda ecuación, tenemos

por lo que  . Así, la solución es
. Así, la solución es  y
y  .
.

Antes de aplicar el método de igualación, debemos escribir el sistema de forma que despejemos una de las variables. Para ello, multiplicamos ambas ecuaciones por 2:

Despejamos la variable y en ambas ecuaciones:

Igualando las ecuaciones, tenemos

por lo que

de manera que  . Luego, sustituyendo
. Luego, sustituyendo  en la primera ecuación, tenemos
en la primera ecuación, tenemos

por lo que  . Así, la solución es
. Así, la solución es  y
y  .
.

Primero despejamos  de ambas ecuaciones
de ambas ecuaciones


Igualando las ecuaciones, tenemos

por lo que

de manera que  . Luego, sustituyendo
. Luego, sustituyendo  en la segunda ecuación, tenemos
en la segunda ecuación, tenemos

por lo que  . Así, la solución es
. Así, la solución es  y
y  .
.
Resolución por reducción
Recordemos que el método de reducción debemos eliminar las  de todas las ecuaciones, excepto la primera. Luego debemos eliminar las
de todas las ecuaciones, excepto la primera. Luego debemos eliminar las  de todas las ecuaciones, excepto la primera y la segunda ecuación.
de todas las ecuaciones, excepto la primera y la segunda ecuación.
Este método es igual a la eliminación gaussiana, con la única diferencia de que no utilizamos la matriz asociada al sistema.

Necesitamos eliminar las  de la segunda ecuación. Para ello, multiplicamos la primera ecuación por
de la segunda ecuación. Para ello, multiplicamos la primera ecuación por  y luego restamos el resultado a la segunda ecuación:
y luego restamos el resultado a la segunda ecuación:

Ahora, a la segunda ecuación le resultamos la ecuación anterior:

De aquí se sigue que  . Luego, sustituimos el valor de
. Luego, sustituimos el valor de  en la primera ecuación:
en la primera ecuación:

Por lo tanto  .
.

Antes de aplicar el método de reducción, debemos escribir el sistema de forma que los términos independientes estén del lado derecho. Para ello, multiplicamos ambas ecuaciones por 2:

Luego, pasamos las variables al lado izquierdo de las ecuaciones:

Ahora, a la segunda ecuación le sumamos la primera:

De aquí se sigue que  . Luego, sustituimos el valor de
. Luego, sustituimos el valor de  en la primera ecuación:
en la primera ecuación:

Por tanto, la solución es  y
y  .
.

Multiplicamos la primera ecuación por  y la segunda por 2
y la segunda por 2


Ahora, sumamos ambas ecuaciones

De aquí se sigue que  . Luego, sustituimos el valor de
. Luego, sustituimos el valor de  en la primera ecuación:
en la primera ecuación:

Por lo tanto  .
.

Antes de aplicar el método de reducción, debemos escribir el sistema de forma que los términos independientes estén del lado derecho. Para ello, multiplicamos la primera ecuación por 4 y despejamos

Ahora, a la segunda ecuación le sumamos la primera:

De aquí se sigue que  . Luego, sustituimos el valor de
. Luego, sustituimos el valor de  en la segunda ecuación:
en la segunda ecuación:

Por tanto, la solución es  y
y  .
.

Antes de aplicar el método de reducción, debemos escribir el sistema de forma que los términos independientes estén del lado derecho. Para ello, multiplicamos ambas ecuaciones por 6 y 9 respectivamente

Ahora, a la primera ecuación le restamos la segunda:

De aquí se sigue que  . Luego, sustituimos el valor de
. Luego, sustituimos el valor de  en la segunda ecuación:
en la segunda ecuación:

Por tanto, la solución es  y
y  .
.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Como puedo solucionar
Y: -3x+2
como puedo resolver el siguiente sistema de ecuaciones
3x+4y+5z=35
2x+5y+3z=27
2x+ y+ z=13
Cómo puedo resolver la siguiente ecuación con el método Gauss – Jordan
5x-10y = 5x+20
[7x-3y=2 3x+4y=-15
I+y=5
I-y=1
3x_y=1
x+y+z=2
5x+7y_3z=3
Metodo de gauss
Como de resuelve esté problema asisten a un congreso internacional de ortopedia en nuestro país 2310 delegados de los que 1/5 son africanos 1/6 de América latina 1/7 de asia 3/11 de Europa
HOLA PRIMERA VEZ QUE ME CONECTO…SOY ANDREA…TEGO ENCONVENIENTE CON ESTE EJERCICIO…SISTEMAS DE ECUACIONES LINEALES…CORCHETE…Y igual3x+1,…X igual 3¡…