Capítulos
¿Cómo podemos usar la programación lineal en la vida diaria?
La programación lineal se utiliza cuando buscamos la solución más óptima para un problema de la vida de cada día, considerando las restricciones. Para poder encontrar la solución, necesitamos formular un problema de la vida real usando un modelo matemático. En los próximos ejercicios de programación lineal, buscamos por una parte, la solución ideal para minimizar el coste de una empresa de transporte, y por la otra, para minimizar el coste de una excursión de escuela.
Problemas de programación lineal
Una empresa de transportes tiene dos tipos de camiones, los del tipo A con un espacio refrigerado de 
y un espacio no refrigerado de 
. Los del tipo B, con igual cubicaje total, al 
de refrigerado y no refrigerado. La contratan para el transporte de 
de producto que necesita refrigeración y 
de otro que no la necesita. El coste por kilómetro de un camión del tipo A es de 
€ y el B de 
€. ¿Cuántos camiones de cada tipo ha de utilizar para que el coste total sea mínimo?
1 Elección de las incógnitas.
camiones de tipo A
camiones de tipo B
2 Función objetivo
3 Restricciones
A
B
Total
Refrigerado
20
30
3 000
No refrigerado
40
30
4 000
4 Hallar el conjunto de soluciones factibles
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
6 Calcular el valor de la función objetivo
Como 
e 
han de ser números naturales redondeamos el valor de .
Por defecto, veamos que valor toma la para 
en la ecuación 
que pertenece al recinto de las soluciones factibles; 
. Obtenemos un número natural
El coste mínimo son 
€ para 
y 
.
Una escuela prepara una excursión para 
alumnos. La empresa de transporte tiene 
autobuses de 
plazas y 
de 
plazas, pero sólo dispone de 
conductores. El alquiler de un autocar grande cuesta 
€ y el de uno pequeño 
€. Calcular cuántos autobuses de cada tipo hay que utilizar para que la excursión resulte lo más económica posible para la escuela.
1 Elección de las incógnitas. autobuses pequeños
autobuses grandes
2 Función objetivo
3 Restricciones
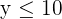
4 Hallar el conjunto de soluciones factibles
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
6 Calcular el valor de la función objetivo
€
€
€ Mínimo
El coste mínimo es de 
€, y se consigue 
autobuses grandes y 
pequeños.
Una fábrica de textiles produce dos tipos de prendas A y B con concentraciones distintas de poliéster y algodón. La prenda del modelo A requiere onzas de poliéster y 
de algodón, mientras la prenda del modelo B necesita onzas de poliéster y 
de algodón. La empresa cuenta con 
onzas de poliéster y 
de algodón. La utilidad marginal de la prenda A es de € y de cada prenda B es de 
€. Determina la cantidad óptima de unidades de prendas A y B que deben fabricarse para maximizar la utilidad por la venta de las prendas.
1 Elección de las incógnitas. número de prendas del modelo A
número de prendas del modelo B
2 Función objetivo
3 Restricciones
4 Hallar el conjunto de soluciones factibles
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
6 Calcular el valor de la función objetivo
€
€
€
€
La utilidad máxima posible es de 
€, y ocurre cuando los niveles de producción son de 
y prendas de los modelos A y B, respectivamente.
En la misma fábrica del ejercicio 3 cambiamos las utilidades. En una fábrica se producen produce dos tipos de prendas A y B con concentraciones distintas de poliéster y algodón. La prenda del modelo A requiere onzas de poliéster y de algodón, mientras la prenda del modelo B necesita onzas de poliéster y de algodón. La empresa cuenta con onzas de poliéster y de algodón. La utilidad marginal de la prenda A es de € y de cada prenda B es de 
€. Determina la cantidad óptima de unidades de prendas A y B que deben fabricarse para maximizar la utilidad por la venta de las prendas.
1 Elección de las incógnitas. número de prendas del modelo A
número de prendas del modelo B
2 Función objetivo
3 Restricciones
4 Hallar el conjunto de soluciones factibles
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
6 Calcular el valor de la función objetivo
€
€
€
€
Los valores óptimos son todos los puntos del segmento de recta 
que se encuentra sombreado; así el problema tiene soluciones óptimas alternativas que producen una utilidad máxima de €.
En una granja se considera servir a los animales dos alimentos cada uno con contenido nutricional distinto. El primer alimento contiene 
de aminoácido tipo 1 y 
de aminoácido tipo 2, mientras que el segundo alimento contiene 
de aminoácido tipo 1 y 
de aminoácido tipo 2. El costo por gramo del alimento 1 es de 
€ y el costo por gramo del alimento tipo 2 es de 
€. Se puede servir cualquier combinación de los alimentos siempre y cuando se sirva al menos tres onzas del alimento tipo 2. Si la cantidad mínima diaria de aminoácido tipo 1 es de 
y de 
, calcule el número de onzas que deben servirse a cada animal, de manera que el costo del alimento sea el más económico.
1 Elección de las incógnitas.
número de gramos del alimento 1
número de gramo del alimento 2
2 Función objetivo
3 Restricciones
4 Hallar el conjunto de soluciones factibles
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
6 Calcular el valor de la función objetivo
€
€
El valor óptimo es 
. Por tanto, el costo mínimo de la comida de cada animal es de 
€, lo cual sucede cuando se sirven 
onzas de alimento tipo 1 y 
onzas del tipo 2.
Un comerciante acude a comprar peras y manzanas con 
€. El productor le ofrece las peras a 
€ el kilogramo y la manzana a 
€ el kilogramo. Se sabe que en su vehículo solo puede transportar 
como máximo y piensa vender el kilogramo de pera a 
€ y de manzana a 
€. El comerciante debe poner a disposición de sus clientes al menos 
de peras. Encuentra la cantidad en kilogramos de frutas que debe adquirir el comerciante para su venta de manera que maximice su utilidad.
1 Elección de las incógnitas.
número de kilogramos de pera
número de kilogramos de manzana
2 Función objetivo
3 Restricciones
4 Hallar el conjunto de soluciones factibles
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
6 Calcular el valor de la función objetivo
€
€
€
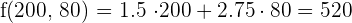El valor óptimo es 
y produce una utilidad máxima de 
€.
Una empresa dedicada a la producción de artículo decorativos cuenta con 
unidades de material y 
horas de mano de obra. Para producir el primer tipo de artículo decorativo se requiere unidades de material y horas de trabajo; para producir el segundo tipo de artículo se requieren unidades de material y horas de mano de obra. La ganancia que obtiene por el primer artículo es de 
€ y de 
€ por el segundo. Encuentra la cantidad de artículos de ambos tipos que deben fabricarse para maximizar las ganancias si la empresa prometió construir al menos un artículo del primer tipo.
1 Elección de las incógnitas.
número de artículos decorativos de tipo 1
número de artículos decorativos de tipo 2
2 Función objetivo
3 Restricciones
4 Hallar el conjunto de soluciones factibles
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
6 Calcular el valor de la función objetivo
€
€
€
El valor óptimo es 
y produce una máxima de 
€.
¿Buscas un profesor de matematicas a domicilio? ¡Encuéntralo en Superprof!
¿Prefieres aprender desde casa? Entra en Superprof, ¡y encuentra ya a tu profesor online de matematicas!
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
una empresa desea maximizar sus ganancias mediante publicidad en television y redes sociales .Cada minuto de television genera 1000 unidades de ganancia y cada hora en redes sociales genera 500.El presupuesto es de 20,000 unidades y los costos son 200 por minuto de television y 1000 por hora en redes sociales .El maximo de horas en reds sociales es de 50 y en televisión es 30
Es un ejemplo de una ecuación utilizada en la programación lineal.
Pregunta 1Respuesta
a.
Y = 23 + 20×2 + 40y
b.
Z = x + 45y
c.
Z = x + 45y3
d.
Y = 20y + 20yx2
Un productor de alimento para animales, fabrica dos clases de grano, A y B. Cada unidad del grano A contiene 2 gramos de grasa, 1 gramo de proteína y 80 calorías. Cada unidad del grano B contiene 3 gramos de grasa, 3 gramos de proteína y 60 calorías. Suponga que el productor desea que cada unidad del producto final tenga, como mínimo, 18 gramos de grasa, 12 gramos de proteína y 480 calorías. Si cada unidad de A cuesta 10 centavos y cada unidad de B cuesta 12 centavos,
¿Cuántas unidades de cada clase de grano debe usar para minimizar el costo?
Alguien me ayuda con este problema: una empresa de transporte se comprometió a transportar 180.toneladas diarias de cemento desde un almacén central a una obra. La empresa tiene 8 camiones de tamaño mediano, cada uno puede transportar hasta 15 toneladas de cemento diariamente y 10 camiones grandes , cada uno puede transportar 20 toneladas de cemento diariamente. La empresa emplea 12 conductores y cada conductor puede conducir cada camión. El gasto diario promedio para un camión mediando es de 400 dolares y para un camión grande es de 600 dolares.
A) cuantos camiones de cada tipo debe manejar la empresa diariamente para que el gasto sea mínimo y aún así la empresa cumpla su compromiso?
B) si el gasto de un camión grande se reduce a 500 dolares. Cual será la respuesta de la pregunta (A).
Una carpintería fabrica dos diferentes modelos de mobiliario A y B. La venta los realiza en $300 y
$200, respectivamente. Para su realización necesita madera, aluminio y hierro. Se cuenta con 1800
m2, 4200m2 y 2100 m2 de cada material. Los consumos de madera, aluminio y hierro para cada tipo
de mobiliario están dados en la siguiente tabla
Madera 200 m3 Aluminio 200 m3 Hierro 300 m3
Madera 100 m3 Aluminio 300 m3 Hierro 100 m3
Una empresa tiene 100 horas de trabajo y $5,000 de presupuesto para producir dos
productos: A y B.
Producto A: 2 horas/unidad, $30/unidad, ganancia de $50/unidad.
Producto B: 3 horas/unidad, $40/unidad, ganancia de $60/unidad.
Objetivo: Maximizar las ganancias.
Restricciones:
2A + 3B ≤ 100 (horas)
30A + 40B ≤ 5000 (presupuesto)
Solver:
Objetivo: Maximizar ganancias = 50A + 60B
Variables: A, B
Restricciones: ≥ 0 y cumplir las ecuaciones anteriores.
me puedes ayudar con un ejercicio de programación lineal unos grandes almacenes desean liquidar 200 camisas y 10 pantalones de la temporada anterior. Para ello lanzan tres ofertas a, b y c la oferta A consiste en consiste en un lote de una camisa y un pantalón , que se venden a 30$ la oferta B consiste en un lote de tres camisas y un pantalón que se venden a 50$ y la oferta C consiste en un lote de 2 camisas y 2 pantalones que se venden en 40 $. no se desea ofrecer menos de 20 lotes de la oferta A ni menos de 10 de la B, ni menos de 15 lotes de la oferta C. ¿cuantos lotes ha de vender de cada tipo para maximizar la ganancia? formule el modelo de programacion lineal.
Este es un problema de optimización lineal. Se puede formular como sigue:
**Variables de decisión:**
* x1: Número de porciones de galleta
* x2: Número de porciones de sorbete
* x3: Número de porciones de refresco
* x4: Número de porciones de pastel de queso
**Función objetivo:**
Minimizar el coste: \[0.5×1 + 0.2×2 + 0.3×3 + 0.8×4\]
**Restricciones:**
* Calorías: \[400×1 + 200×2 + 150×3 + 500×4 ≥ 500\]
* Chocolate: \[3×1 + 2×2 + 0x3 + 0x4 ≥ 6\]
* Azúcar: \[2×1 + 2×2 + 4×3 + 4×4 ≥ 10\]
* Grasa: \[2×1 + 4×2 + 1×3 + 5×4 ≥ 8\]
* No negatividad: \[x1, x2, x3, x4 ≥ 0\]
Para resolver este problema se puede usar el método simplex o cualquier software de optimización lineal. La solución proporcionará los valores óptimos de x1, x2, x3 y x4 que minimizan el coste al tiempo que cumplen todas las restricciones.
Ayuda con este problema
DATOS
Shorts (modelo A):
Requerimiento de poliéster: 10 onzas
Requerimiento de algodón: 2 onzas
Utilidad marginal: $15 por prenda
Faldas (modelo B):
Requerimiento de poliéster: 5 onzas
Requerimiento de algodón: 6 onzas
Utilidad marginal: $12 por prenda
Disponibilidad de recursos:
Poliéster: 400 onzas
Algodón: 250 onzas
Cantidad óptima de Shorts (modelo A): 20 unidades
Cantidad óptima de Faldas (modelo B): 40 unidades AYUDA A RESOLVER